DIALOGUE:
V: Ok, I saw one simulation in java that shows the same result like this!
B: Could program make anything different what we order them to do?
V: I don't understand.
B: Well, program execute some math equation, if we write 2x3 program will multiple it.
V: And, if we use wrong calculation we will get wrong result.
B: Exactly!
V: Then, why we are using them.
B: You mean computers?
V: Yes!
B: Only for faster calculation.
V: And what is wrong here?
B: Let's find out that together. What is idea here?
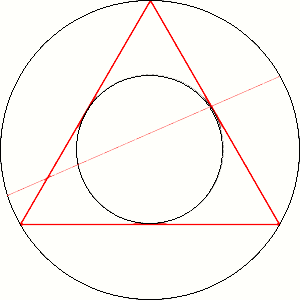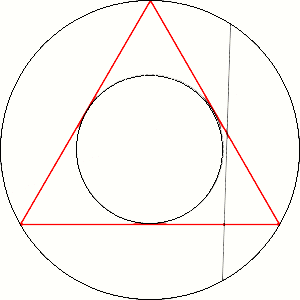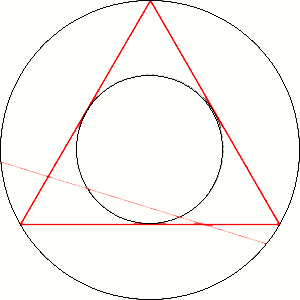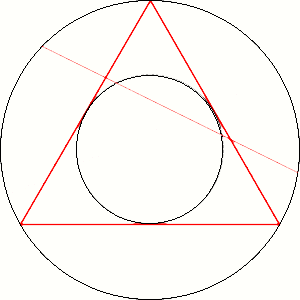
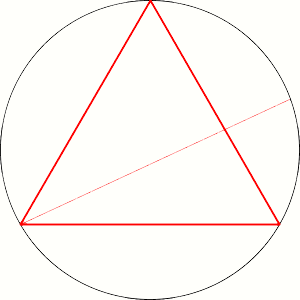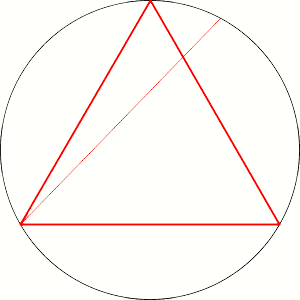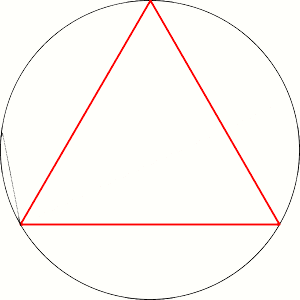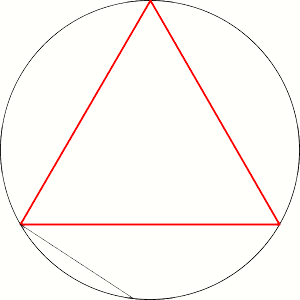
V: One point of the surface of the circle determine middle point of one chord. And if the point stays closer to the center than half the radius then is appropriate chord longer then side of inscribed equilateral triangle.
B: What do you mean, why is radius used here?
V: Because, it includes set of chords from shortest one to longest.
B: Is that only reason?
V: Yes! If it represents set of chords that we have here, that is enough.
B: We can use then and some other line instead radius. Like on the pictures.
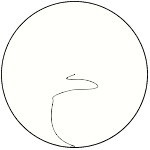
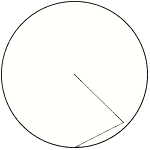
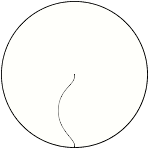
V: But it gives different result.
B: And?
V: It can't covers surface of the circle uniformly. With radius we can calculate on that way because the circle consist of infinity radii.
B: Well, if we can't cover surface uniformly, we can't take that line in calculation?
V: Yes.
B: How we calculate surface of one circle or one part of the circle? How we get the formula for that?
V: With integration.
B: And what we integrate there? Radii?
V: If we integrate radii we will not get formula for surface of the circle!
B: Thus, what?
V: I see! We integrate little sectors.
B: And that isn't the same.
V: No, it is not! But if we leave the angle very small we will get the radius.
B: Only if angle has zero value we will get the radius!
V: Then it is not a sector any more! 100x0 equals 0, and we can't make sector.
B: So, could we cover with infinity radii circle shape.
V: No, we can't! Then is all wrong, and it is the same as we use that curves above for calculation.
B: Correct!
V: So, we must calculate with sectors, to make in summary a circle?
B: That is problem of second example, let's go there.
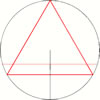 First solution:
First solution: First solution:
First solution: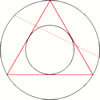 Second solution:
Second solution:  Third solution:
Third solution: 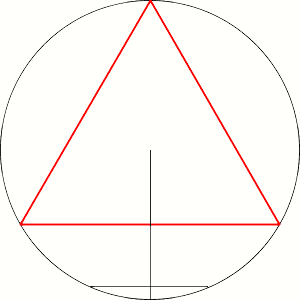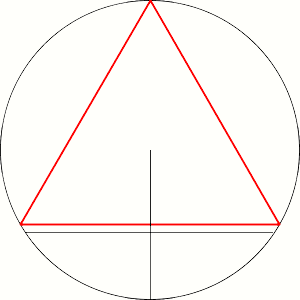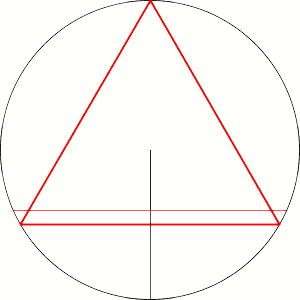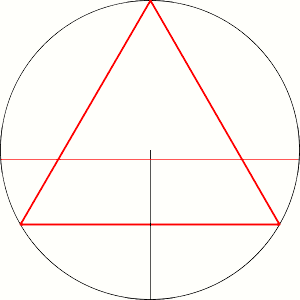




I did not understand yor statment well. You sad:"you are generating chords based on polar coordinates from an arbitrary orgin, weighting the area near the orgin far more heavily than the rest of the circle". In respect to what I weighted some chords in calculation?
Your example involves presumption that longer chords have more probability to be chosen because they consist more points (among diametar we can choose more points to determine one chord than in other direction). Why? In that case each chord is not equaly probable and we are changing the original problem! It is not allowed. Do you agree?
Consider similar problem where the circumference is not closed, where small part "dl" of it is missing (like shape of the letter "C"). How can you connect area with the number of chords then? So, here is crucial not to make fake transformation. If you have to count chords you can do it via area only if you are able to prove that transformation as bijection (one to one transformation).
Thanks for your comment Brian!
So, if we say that each chord is determined with its mid-point (and they are spread over all surface of the circle) and chords that have lenght longer then critical have mid-points only inside circle with two times smaller diametar, probability becomes p=(R2/4)/(R2)=1/4.
Yes ... probability just for mid-point is zero, but that point represent infinite!!! number of chords, so that model where we do nut substitute one chord with one point (or finite number of chords) can't be discussed as option for resolving our problem (and any other problem in probability without using appropriate jacobians)!
What is probability of getting numbers 4,5,6 using fair cube (dice)? With your model of probability (p=(one set of elements)/(second set of elements)) becomes p=1!. p=3/3=1 and that doesn't have any sense.
Ok, let's rotate our circle for 90 degrees around y axis. Now, after one additional nonlinear tranformation we can see one straight line and probability is p=(2xR/2)/(2R)=1/2 !? I doubt that you will say p=1/1=1. How would you correct it now?